技术揭秘：如何解决 MOE 模型 RL 训练的不稳定性？#

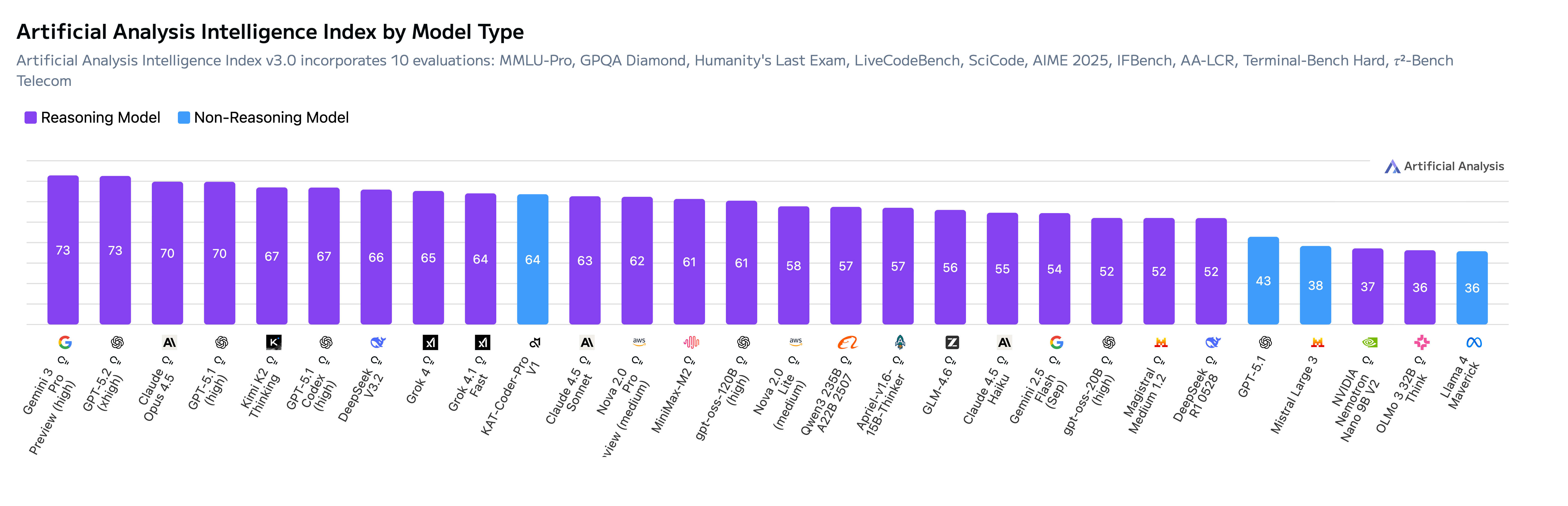
当前业界大多把模型在RL训练时出现reward 崩溃的问题归因于“训推不一致”。然而，我们的实验发现：当前阶段 RL 训练不稳定的主导因素并不是训推不一致，而是采样噪声（Sampling Noise）本身。当我们显式抑制噪声强度后，即使存在明显的训推差异，训练依旧保持稳定，并能获得更快的收敛速度。基于此技术，KAT-Coder-Pro V1经过我们大规模agentic RL后，其综合能力得以与世界头部的模型相比肩，在权威评测机构 Artificial Analysis（AA）榜单中表现亮眼，以 64 分综合评分跻身全球总榜TOP 10，更以绝对优势在 Non-Reasoning Model 中斩获第一名。

当前重要性采样的实现方式：偏差–方差视角#

在off-policy场景中，策略梯度算法同时使用重要性采样技术：

\nabla J(\theta) = \mathbb{E}_{a \sim \pi_{\text{rollout}}} \left[ R(a)\, \frac{\pi_{\text{train}}(a)}{\pi_{\text{rollout}}(a)}\, \nabla_\theta \log \pi_{\text{train}}(a) \right]

在理论上， $\pi_{\text{rollout}}$ 和 $\pi_{\text{rollout}}$ 表示推理策略和训练策略的真实动作概率分布。然而在 LLM RL 的实际实现中，我们只能获得其带噪声的观测值 $\widehat\pi_{\text{rollout}}=\pi_{\text{rollout}}+\epsilon_{rollout}$ 和 $\widehat\pi_{\text{train}}=\pi_{\text{train}}+\epsilon_{train}$ ，该噪声由数值精度、并行原子操作、kernel选择的不确定性等因素共同导致[1]。重要性采样中的比值 $\frac{\widehat{\pi}_{\text{train}}}{\widehat{\pi}_{\text{rollout}}}$ 因此包含了额外的方差，采样噪声 $\epsilon$ 成为 RL 训练不稳定的主要来源之一。我们测量了同一 token 序列下，推理引擎与训练引擎输出的logprob的统计差异：

模型类型	$\text{diff}(\widehat{\pi}_{\text{train}}, \widehat{\pi}_{\text{rollout}})$	$\operatorname{var}(\epsilon_{\text{rollout}})$	$\operatorname{var}(\epsilon_{\text{train}})$
Dense	$\sim 0.002$	$\sim 10^{-5}$	$0$ （Megatron deterministic）
MoE	$\sim 0.008$	$\sim 10^{-3}$	$10^{-7}$ （induced by the stochastics of `scatter_add`）

当前主流的RL训练框架为了降低 $\widehat\pi_{\text{rollout}}$ 的采样噪声都会在rollout结束后使用训练引擎（如，Megatron或FSDP）对采样token重新计算其logprob： $\widehat\pi_\text{recompute}(a)={Training\_Engine}(a)$ （注意， $\widehat\pi_{\text{recompute}}\equiv\widehat\pi_{\text{train}}$ ，前者特指当用训练引擎计算logprob用作重要性采样分母，后者作为重要性采样的分子）。这一方法相比直接用 $\widehat\pi_{\text{rollout}}(a)$ 作为分母来说训练效果更好。由于 $var(\epsilon_{\text{rollout}})$ 较大，仅用一次推理引擎的采样进行计算，采样噪声会使得策略梯度方差显著增大，导致训练收敛慢甚至崩溃。而将 $\widehat\pi_{\text{recompute}}$ 作为分母，对于dense模型来说，其 $var(\epsilon_{\text{train}})$ 为0，并且 $\widehat\pi_{\text{train}}$ 与 $\widehat\pi_{\text{rollout}}$ 的差异很小。因此 $\widehat\pi_{\text{recompute}}(a)$ 可作为 $\pi_{\text{rollout}}(a)$ 的偏差方差均较低的估计器，从而保证了训练的稳定性。

但该方法在MOE模型上会有问题，这是因为MOE模型的专家选择会显著放大训练和推理的不一致性， $\widehat\pi_{\text{recompute}}$ 与 $\widehat\pi_{\text{rollout}}$ 的期望偏差也显著增大(0.002 —> 0.008)。这种偏差的增大，会显著影响用重计算作为估计器的RL训练，而且随着训练进行，这种误差也会随之累积，进而导致训练崩溃。

因此，在重要性RL稳定训练的关键是如何获得一个偏差和方差都尽可能小的 $\pi_{\text{rollout}}$ 估计器。

多次采样估计法#

我们提出一种简单有效的做法：

在计算 old_logprob 时，使用推理引擎重复计算同一输入 n 次，并对结果取平均：

\hat{\pi}_{\text{rollout}} = \frac{1}{n} \sum_{i=1}^{n} \pi_{\text{inference}}^{(i)}

从而得到无偏且方差缩小n倍的 $E[\pi_{rollout}]$ 的估计。这一方法不依赖routing replay，也无需复杂缓存机制，适用于 MoE 与多轮交互场景。此外，我们的方法无需使用训练引擎重新计算 $\pi_{recompute}$ ，而且在异步框架下，多次采样计算 $\hat\pi_{rollout}$ 的时间可以与rollout时间重叠，从而掩盖多次计算 $\pi_{inference}$ 的时间，并且KV cache命中率接近100%。从端到端延迟来看，这种多次采样的做法反而可以减少10%～20%的训练时间。

重新审视当前稳定RL训练的几种方法#

1. Routing Replay#

在重计算 logprob 时强制使用 rollout 阶段的专家路由。通过固定专家路由，可以满足：

$var(\pi_{recompute})$ 较小；
$E(\pi_{recompute})\approx E(\pi_{rollout})$ 。例如 R3（rollout routing replay）[2] 提出的在Prefix Cache中保存routing mask的方法理论上可以实现此功能，但在大规模agentic场景下难以保证Prefix Cache始终命中。若要保证Prefix Cache全部命中，实现成本过高且rollout吞吐率将大幅下降。

2. 截断重要性采样（TIS）#

\nabla J(\theta) = \mathbb{E}_{a \sim \pi_{\text{rollout}}(\theta_{\text{old}})} \left[ \min\!\left( \frac{\pi_{\text{recompute}}(a, \theta_{\text{old}})}{\pi_{\text{inference}}(a, \theta_{\text{old}})},\, C \right) \cdot \nabla_{\theta} \min\!\left( \frac{\pi_{\text{train}}(a, \theta)}{\pi_{\text{recompute}}(a, \theta_{\text{old}})} \, \hat{A}, \operatorname{clip}\!\left( \frac{\pi_{\text{train}}(a, \theta)}{\pi_{\text{recompute}}(a, \theta_{\text{old}})},\, 1-\epsilon,\, 1+\epsilon \right) \hat{A} \right) \right]

重计算方案由于训推不一致问题导致IS出现偏差，TIS[3]的思路是再做一次IS来修正训推之间的偏差，同时对其数值范围设置上下界，从而削弱极端重要性采样权重对梯度的影响。这种方法不需要缓存专家路由，在实现上相对简单。然而，它只能从表面上缓解方差爆炸问题，并不能解决 $\pi_{rollout}$ 本身估计不准的根本原因。而且，方法的效果对截断上下界的选取十分敏感，选择稍有不当就可能导致偏差过大或收敛停滞。在复杂的 MoE 模型或多轮交互任务中，TIS 的效果也往往不稳定。

3. 确定性推理#

除了从算法角度降低 $\hat{\pi}_{\text{rollout}}$ 的方差（如我们提出的多次前向平均），采样噪声也可以从infra层面被直接消除。近期，vLLM 与 SGLang 分别实现了确定性推理，使推理端在相同输入下输出完全一致的 logits 与 log-prob，同时保证训练和推理log_prob的比特级一致，从源头降低 $\pi_{\text{inference}}$ 的方差和偏差。

但这些方案的代价也很明显：为实现确定性推理，需要对推理引擎进行深度改造，工程成本较高；同时，许多高性能优化无法继续使用，实际推理吞吐率也会下降40～70%。相比之下，我们提出的低方差采样估计方法无需修改推理引擎，并且额外引入的推理成本可与 rollout 截断其他轨迹的推理时间重叠，在获得相似稳定性的同时保持极低的工程成本与更高的训练效率。

实验#

我们在 Qwen3-235B-A22B 模型上系统验证了不同重要性采样估计策略对强化学习训练稳定性的影响。实验环境采用主流 RLHF 框架VERL，保持相同的训练数据和超参数设定，仅更换旧策略概率 $\pi_{\text{rollout}}$ 的计算方式，以便公平比较。

我们对比了以下四种典型方案：

TIS（Truncated Importance Sampling）：在计算重要性权重w(a)时设置上下界（clipping），以控制方差放大。
使用推理引擎采样概率（rollout_logprob）：使用 rollout 阶段推理引擎输出的 $\pi_{\text{sampler}}$ 作为 $\pi_{\text{rollout}}$ 。
训练引擎重新计算概率（recompute_logprob）：在 rollout 结束后，利用训练后端重新计算 $\pi_{\text{learner}}$ 并作为旧策略概率。
Routing Replay：在重计算阶段强制复用 rollout 阶段的专家路由，以减少路由随机性造成的波动。

我们的多次采样估计法（Ours）：对同一输入重复前向n=8次，取平均概率作为旧策略概率。

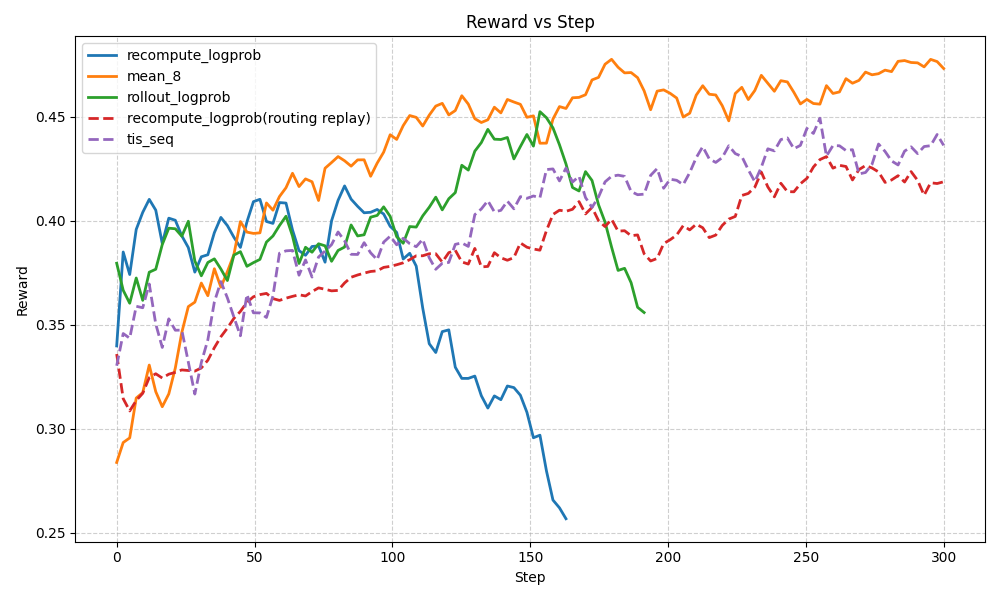
图1 展示了不同方法在训练过程中的 reward 变化曲线。可以观察到： line_graph

recompute_logprob、rollout_logprob 两种方法均在训练后期出现明显的 reward 崩溃或震荡放大现象，实验中具体表现为 reward 在 60~80 step 之后快速下降，并无法逆转。
Routing Replay 在一定程度上缓解了崩溃，reward 能始终保持相对稳定。但实现时为了避免rollout吞吐大幅下降，在多轮场景下无法保证prefix cache 100%命中，因此其效果无法达到最优。
TIS和我们的低方差采样估计方法则在整个训练过程中保持稳定增长。TIS相比我们的方法对超参数的设置更敏感，在一些参数设置下也可能存在崩溃，或收敛速度下降的问题。我们的多次采样估计法无需设置超参，并且reward涨势也明显比TIS更好。

此外，为了验证我们的方法确实能够有效降低 $\hat{\pi}_{\text{rollout}}$ 和 $\pi_{\text{train}}$ 之间的偏差，我们统计了训练过程中两者之间的KL散度，如下图所示：

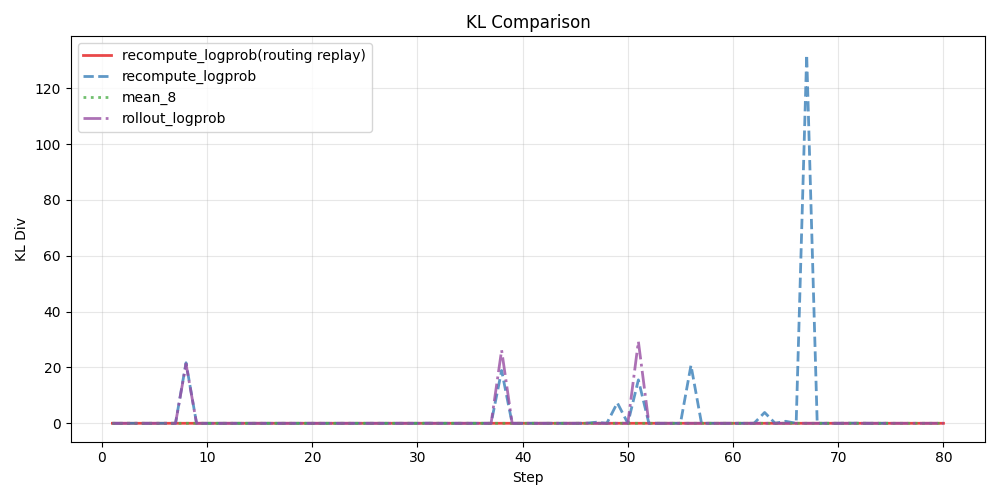kl_compare 从图中可以看出，不管是使用训练引擎重新计算logprob还是直接使用推理引擎的logprob，都会在训练过程中出现KL散度的剧烈波动，而routing replay和我们的低方差采样概率估计都能在整个训练过程中将KL散度保持在较低水平。

references：

[1] He, Horace and Thinking Machines Lab, “Defeating Nondeterminism in LLM Inference”,

Thinking Machines Lab: Connectionism, Sep 2025.

[2] @misc{ma2025stabilizingmoereinforcementlearning, title={Stabilizing MoE Reinforcement Learning by Aligning Training and Inference Routers}, author={Wenhan Ma and Hailin Zhang and Liang Zhao and Yifan Song and Yudong Wang and Zhifang Sui and Fuli Luo},year={2025},eprint={2510.11370},archivePrefix={arXiv},primaryClass={cs.CL},url={https://arxiv.org/abs/2510.11370},}

[3]@misc{yao2025offpolicy, title = {Your Efficient RL Framework Secretly Brings You Off-Policy RL Training}, url = {https://fengyao.notion.site/off-policy-rl}, author = {Yao, Feng and Liu, Liyuan and Zhang, Dinghuai and Dong, Chengyu and Shang, Jingbo and Gao, Jianfeng}, journal = {Feng Yao’s Notion}, year = {2025}, month = aug, }

Please cite this work as:

@article{kk2025moerlsamplingnoise,

author = {KwaiKAT Team},

title = {Reducing Sampling Noise to Improve Stability of MoE Reinforcement Learning},

year = {2025},

url = {https://kwaikat.github.io/kwaikat-blog/posts/katcoder_1201/} }

Contacts: zhangxiaojiang@kuaishou.com, wangjinghui05@kuaishou.com